The Fallacy of Fencelessness, Why Cage Free is Best Part 2
By Alberto Moel (Vice President Strategy and Partnerships)
Welcome back, dear reader, to a follow-on discussion on how “fencelessness” and collaborative robotics aren’t necessarily the ideal mix. In Part 1 we reviewed how, depending on robot speed and stopping times, a truly “fenceless” collaborative application may require an uneconomically large workcell area for safe operation.
This large workcell area is needed as a buffer zone between the robot and an approaching human so that the robot can slow down and stop safely before the human arrives. Our proposal in Part 1 was that the judicious use of fencing to constrain human motion is both economically superior and allows for better human-robot interaction. This is because we can only control the speed and trajectory of the robot and not that of humans in the vicinity, and we have to be quite conservative and assume a human may approach the robot directly at high speed, hence the need for a buffer area.
In this post we’ll delve a little deeper on how that buffer area changes with robot velocity, some practicalities on the estimation of the Protective Separation Distance (PSD), and how the use of fences reduces the sensitivity of the workcell design to the application parameters, in particular to robot velocity. Our analyses will show that physically constraining how humans can enter and exit a workcell makes manufacturing applications space efficient and robust to changes in robot trajectories and velocity.
Figure 1. Unfenced and fenced versions of a simple operator load station application with a keep-in zone and a robot operating at 66% of full TCP speed (at 66% of maximum payload).
Figure 1 shows the two options we discussed—“fenceless” on the left, and with two fences on the right, where the robot envelope is safely constrained to a 2.8x3.5m “keep-in” zone defined using FANUC’s Dual Check Safety (DCS) system. Using the stopping time data provided by FANUC for the R2000iC/165F robot, we calculated a Protective Separation Distance (PSD) of 1.52m for 66% of full TCP speed, with an assumed payload of 110kg (66% of payload limit).
By constraining the workcell’s entry points from 360 degrees to a couple of specific locations as shown on the right of Figure 1, we can reduce the area of the workcell to 18.3m2, which is less than half that of the unconstrained “fenceless” area of 38.2m2.
Robot velocity, PSD, and fenceless workcell area
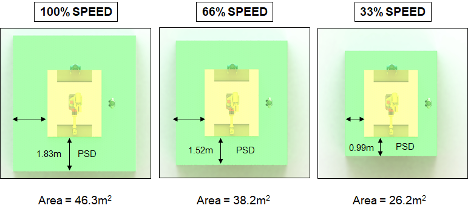
Figure 2. PSD and required workcell area for an unfenced workcell as a function of maximum robot TCP speed (at 66% of maximum payload).
Clearly, the PSD is a function of the robot velocity, payload, and pose, and robot manufacturers provide graphs and data points for stopping times and distances as a function of speed, payload, and arm extension, which are necessary for the correct implementation of Speed and Separation Monitoring (SSM) and calculating the PSD.
An obvious question is the relationship between robot velocity and PSD. Figure 2 shows graphically the PSD and required buffer zone for the fenceless workcell as a function of maximum robot velocity, calculated from stopping time and distance data provided by FANUC.
Clearly, the required workcell area is a simple function of the PSD, so if we are able to calculate the PSD, determining the workcell area is a quick exercise. But how is the PSD calculated? From ISO 10218-1, the PSD can be estimated by
where
Sp(t0) is the PSD at time t0;
t0 is the present or current time;
th is the contribution to the protective separation distance attributable to the human’s change in location;
Sr is the contribution to the protective separation distance attributable to the robot system’s reaction time;
Ss is the contribution to the protective separation distance due to the robot system’s stopping distance;
C is the intrusion distance, as defined in ISO 13855; this is the distance that a part of the body can intrude into the sensing field before it is detected;
Zd is the position uncertainty of the operator in the collaborative workspace, as measured by the presence sensing device resulting from the sensing system measurement tolerance;
Zr is the position uncertainty of the robot system, resulting from the accuracy of the robot position measurement system.
ISO 10218-1 Annex B requires that the stopping time and distance for different dynamic states of the robot (at a minimum, 33%, 66%, and 100% of speed, load, and extension, respectively) be provided by robot manufacturers. However, these data are often fragmented, hard to interpret, overly conservative, and sometimes generated by simulation. The requirement itself is interpreted differently by different robot manufacturers—some provide these data in tables of different sparseness, while others provide it in graphs that vary in resolution quality.
For example, ISO 10218-1 only states that data should be provided for those three speeds, the lowest being 33%, and there is no guidance around how to extrapolate down to zero speed. In some cases the published stopping data indicates that it will take the same amount of time for the robot to stop whether it is moving at 33% speed with 33% load, 100% speed with 100% load, or any combination in between. This is likely because the worst-case number for 100% speed and 100% load was propagated throughout the table.
Taking controller latencies into account with the published data provides a low level of certainty for the final stopping position of the robot. With the limited data available, the "worst-case" PSD calculation for SSM is functional but much less precise and more conservative than warranted by the robot dynamics and the control system latencies. Without access to planning information used by robot controllers (which uses such data to determine precisely how robot motion will cease), the uncertainty represented in the PSD calculated from manufacturer-provided data prevents the closest and most efficient collaborative operation.
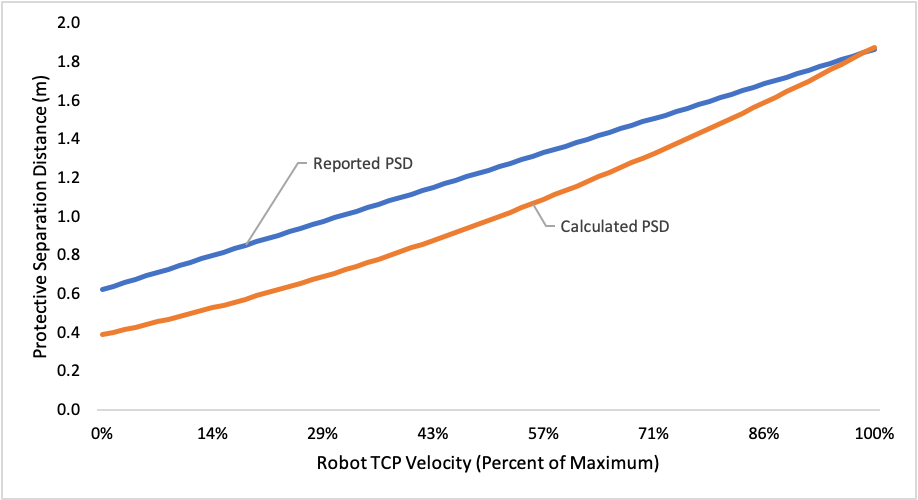
Figure 3. PSDs estimated from reported stopping times for the FANUC R2000iC/165F and calculated from first principles derived from latency and kinematic assumptions as a function of robot speed for 66% payload.
As an example, Figure 3 shows our estimate of the PSD from reported stopping distance for the FANUC R2000iC/165F, and our calculated PSD using the equation above and some sensible (and likely conservative) assumptions about robot kinematics, robot controller and sensor latencies, and encoder and sensor noise.1
As mentioned, the PSD estimated from the provided stopping time data is generally larger than the calculated PSD, with the gap decreasing the faster the robot is moving. It seems that the reported stopping time data assumes very fast deceleration (as would be the case with a Category 0 stop) and a long delay (in the order of hundreds of milliseconds) between the time the stop signal is enabled and the robot begins stopping. Under more “relaxed” deceleration conditions, the stopping distance will increase quadratically with initial velocity and we should see a faster than linear decline in stopping distance as initial velocity decreases.
And even if the robot is standing still, the PSD is not zero. This makes sense, as the PSD needs to incorporate sensor and robot position reporting latencies and encoder and sensor uncertainty. For example, in the case of the Veo FreeMove system, latency between the sensor capture and robot control signal is 133ms. In that span of time, a human traveling at 1.6-2.0m/sec can move 20-30cm, so at a minimum a PSD of that length is required.
The higher the robot speed, the greater the need for fences
Although the calculated PSD from reported stopping time data is (more or less) a linear function of velocity, workcell geometry would imply that the workcell area increases quadratically with top robot velocity.
Figure 4. Calculated required fenceless and 2-fence workcell area as a function of robot speed for 66% payload, using the PSD estimated from reported stopping time data.
Figure 4 shows a comparison of the required workcell area between a fully fenceless workcell and one constrained by two fences as described here. The PSD is calculated using the reported robot stopping distances (the blue line in Figure 3). Depending on the maximum robot speed, workcell area savings range from 31% (for the robot standing still) to 57% at maximum robot velocity. Clearly, judicious placement of guarding meaningfully reduces the required workcell areas of collaborative applications.
Figure 5. Calculated required fenceless and 2-fence workcell area as a function of robot speed for 66% payload, using the PSD estimated from first principles.
Figure 5 shows the same analysis but using the estimated PSD from first principles kinematics and latencies (the orange line in Figure 3). The required workcell area is overall smaller and the effect of speed on the workcell area more pronounced, as now the PSD is a convex function of robot velocity (as opposed to a linear function using the reported stopping times).
Of course, it would be preferred if PSDs could be reduced even further, and perhaps decoupled from robot speeds, payloads, or poses. What is in the pipeline to get us there? At Veo Robotics, we are working with our robot partners in finding truly fluid human-robot collaboration, and reducing the PSD is a major focus. How to do so by better characterizing robot controller latencies and application-specific robot dynamics will be the subject of subsequent blog posts, so stay tuned.
1If you must know, here are some numbers for you. As required by the standard, we assume humans move at 1.6m/sec, robot position data is streamed at 4ms, the Veo FreeMove sensor has a latency of 133ms, and the robot can decelerate at 10m/sec2.